「『場合の数』で急に『二項定理』って出てきたけど、何なの?」という高校生の方へ。東大卒講師歴20年の管理人がわかりやすくまとめました。
目次(クリックでジャンプ)
二項定理
(x+y)3を展開した時の「x2y」の係数はいくつかというと、公式「(x+y)3=x3+3x2y+3xy2+y3」を思い出せば「3」と分かります。
しかし (x+y)10を展開した時の「x2y8」の係数はいくつになるかは公式を覚えていないし実際に展開するのは面倒くさいですね。これを簡単な計算で求めるのが二項定理です。
定理を導く
(x+y)3を展開した時の「x2y」の係数がどう決まるか考えてみます。
(x+y)3=(x+y)(x+y)(x+y)なので、これを展開してできる項は、3つの(x+y)からxかyのどちらかを選んでかけたもので、
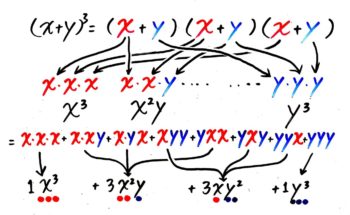
これは「x」「y」と書かれた2つの玉が入った3つの箱から玉を1つづつ合計3つ取り出すようなものです。

そして「x2y」の項は2つの箱からx玉を、1つの箱からy玉を取り出しているので、その取り出し方は3つの箱からxを取り出す2つの箱を選ぶ(または3つの箱からyを取り出す1つの箱を選ぶ)場合の数(組み合わせ)の「3C2」(または「3C1」)=3通りで、係数は3と分かるのです。
要するに、(x+y)3を展開した時の「x2y(1)」の係数は3C2(または3C1)ということです。この時、xとyの累乗の数は勝手に決められず、和が3になっているのも分かります。
この理屈を使って、(x+y)10を展開した時の「x2y8」の係数を求めると、10C2(または10C8)=10×92×1=45と分かります!
(展開で出すかと思うと気が遠くなりますねw)
これを定理の形にしたのが二項定理です。
p+q=nのとき、(a+b)nのapbqの係数はnCq (または nCp)
(理由)n個の(a+b)からaかbを選ぶときに、bをq個(またはaをp個)選ぶ組み合わせの数がnCq(nCp)だから
(例)(x+y)10のx2y8の係数は10C2
別の考え方(この後使います)
教科書には上記の考え方が書いてありますが、もっと単純に次のように考えてもよいでしょう。
「x2y」になる項を展開直後の(降べき順の並べ替えをしていない)形で書くと「xxy」「xyx」「yxx」の3通りで、これが係数3になっています。
そしてこれは「x,x,y」の並び替えなので「同じもの2つ(と1つ)を含む合計3個を並び替えるアルファベット順列」の公式で3!2!×1!=3×2×12×1×1=3 と分かります。
練習問題
(x+y)7を展開したときにx5y2の係数はいくつか?
→( n=7,p=5,q=2 なので、nCp=nCq=7C2=21 )
(2x+3y)7を展開した時のx5y2の係数はいくつか?
注意:単純な nCp=nCqで終わりではない
→( 二項定理で出るのは(2x)5(3y)2 の係数 )
→( 二項定理を計算すると7C5=7C2=21 )
→( 21(2x)5(3y)2 になるので、これを整理して21×32x5×9y2=6048x5y2)
→( 答えは6048 )
次は三項定理です。
三項定理
三項式の累乗、例えば(x+y+z)9を展開した時の「x2y3z4」の係数はいくつになるかを求めるのが三項定理です。
定理を導く
二項定理の「もう一つの考え方」を使えば簡単です。
「x2y3z4」になる項は「x,x,y,y,y,z,z,z,z」の並び替えなので「同じもの2つと3つと4つを含む合計9個を並び替えるアルファベット順列」で9!2!×3!×4!=1260通り と分かります。
これを定理にしたのが三項定理です。
p+q+r=nのとき、(a+b+c)nのapbqcrの係数はn!p!q!r!
(理由) aをp個,bをq個,cをr個含む合計n個の並べ替え(アルファベット順列)だから
(例)(x+y+z)9のx2y3z4の係数は9!2!×3!×4!=1260通り
練習問題
(2020.1.10作成中)
まとめなど
最後に公式を確認テスト形式にしてみました。
●二項定理
p+q=nのとき、(a+b)nのapbqの係数は( nCq (または nCp )
(理由)
n個の(a+b)からaかbを選ぶときに、bをq個(またはaをp個)選ぶ( 組み合わせ )の数がnCq(nCp)だから
(例)
(x+y)10のx2y8の係数は( 10C2 )
●三項定理
p+q+r=nのとき、(a+b+c)nのapbqcrの係数は( n!p!q!r! )
(理由)
aをp個,bをq個,cをr個含む合計n個の並べ替え( アルファベット順列 )だから
(例)
(x+y+z)9のx2y3z4の係数は( 9!2!×3!×4!=1260通り )
これで場合の数は完全に終了です。確率に進んで下さい。
最後まで読んでいただきありがとうございました。この記事があなたの役に立てたなら嬉しいです。
