場合の数の基本公式(順列nPrと組合せnCr)は理解できたけど、円順列とか重複とか…よく分からない!」という高校生の皆さんへ。基本が分かったなら、あとちょっとで応用の公式も理解できますよ♪東大卒講師歴20年の管理人が分かりやすく説明します。記事を読み終える頃には問題を解きたくなっているでしょう!
目次(クリックでジャンプ)
基本の復習
場合の数には、選んで並び替える(順番がある枠に入れる)「順列」と、ただ選ぶだけの「組合せ」の二種類がありました。
●n個からr個選んで並べる nPr
(例)5個から3個選んで並び替える
→ 5P3=5×4×3=60
●n個を並び替える r! (階乗)
(例)5個を並び替える→5!=5×4×3×2×1=120
●n個からr個選ぶ nCr=nPr÷r!
(例)7C2=7×62×1=21通り
●nCr=nCn-r
(例)7C5=7C7-5=7C2
万が一、これらが怪しい場合は「場合の数の基本」を見直したほうがいいかもしれませんね。大丈夫な人は、応用に進みましょう
円順列
ものを円形に並べる場合です。直線に並べる場合とどう違うでしょうか
基本的な考え方
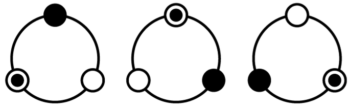
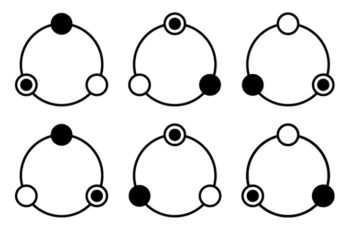
例えば3個を円形に並べる(r=3)場合、単純な3個の並び替え(3!)では3×2×1=6通りになりますが、同じ並び(時計回りに●→○→◉)が3つできるので同じ並びを3通りとして数えていたことになります。したがって本当の答えは 6通り÷3=2通り です。
この「÷3」が重複カウントの処理です。
基本の公式
このように円形にr個並べるとr個を重複カウントするので、n個からr個選んで円形に並べる場合は順列の答えnPrを重複カウントrで割れば良いので、nPr÷r 通りになります。
特にn人全員を円形に並べる時は、同じ形がn個できて重複カウントがnになるので、答えは n!÷n=n×(n-1)×(n-2)…×1n=(n-1)×(n-2)…×1 =(n-1)! になる。
●n個からr個選んで円に並べる
→ nPr÷r 通り
○r個を円に並べる
→ (r-1)! 通り
確認テストをどうぞ
7人から4人選んで丸テーブルに座らせる
→( 7P4÷4=7×6×5×44=7×6×5=210通り )
7人全員を丸テーブルに座らせる
→( (7-1)!=6×5×4×3×2×1=720通り )
数珠順列
縁起が悪い話ですが、数珠は裏も表もありません。裏返したものも一つに数える円順列を数珠順列と呼びます。
円順列に加えて裏返したものも同じと数えるので、r×2パターンを重複カウントしていることになります。
→円順列と比べて重複カウントが2倍なので、答えは円順列の半分(÷2)になる
(反対向きも同じに数える)
→ 円順列÷2 =nPr÷r÷2 通り
→ n個全部を円に並べる時は (n-1)!÷2 通り
確認テスト(2020.1.8作成中)
円順列の応用問題(場所の指定)
自分が「円形テーブルで行われる会議の席順決め係」になって、出席者に指示するつもりで手順を考えます。
誰かの位置が決まった後は、円順列ではなく普通の順列nPrになるのに注意しましょう。
特定の2人の位置を指定する問題
ABCDEFの6人が円に並ぶ場合、AとBが向かい合うのは何通りあるか
→手順①AとBを向かいに座らせる(AとBを固定)。=1通り
→手順②残った4席にCDEFを座らせる(円順列ではない)。4!=24通り
→上記の積 1×24=24通り が答え。
グループの位置を指定する問題
男子ABC女子XYZ合計6人が円に並ぶ場合、男女が交互に並ぶのは何通りあるか?
→手順①まず男子ABC3人を円に並べる。(3-1)!=2通り
→手順②次にそのスキマ3箇所に女子を並べる(円順列ではない)。3!=6通り
→上記の積 2×6=12通り が答え。
確認テスト(2010.1.8作成中)
同じものを含む順列
(アルファベット順列)
例えば、aを3個・bを2個・cを1個含む合計6個の「a,a,a,b,b,c」を並び替えて作れる単語は何通りか考えます。
全部が違う6文字の並べ替えは6!ですが、この問題では同じ種類の文字aが3個あるので3!の重複カウントがあります(前回の記事の「部屋分け問題」を思い出してください)。さらにb2個で2!の重複カウントもあるので、重複カウントは 3!×2! になります。
結局、6文字の並べ替え6!を3!×2!で割った 6!3!×2!=6×5×4×3×2×13×2×1×2×1=60通り が答えになります。
このように、同じ種類のものp個q個…を含む合計x個のものを並べ替えるとx!をp!×q!で割ったものが答えです。→x!p!×q!…
このタイプは「同じものを含む順列」と呼ばれていますが、呼びづらいし愛着がわかないので、勝手に「アルファベット順列」と名付けました!
●同じ種類のものp個q個…を含む合計x個のものを並べ替える
→x!p!×q!… 通り
この順列は応用が効いて便利なのでサッと解けるようにして下さい。
xを2個・yを2個・Zを2個含む合計6個の「x,x,y,y,z,z」を並び替えて出来る単語は何通りか?
→( 公式にあてはめて、6!2!×2!×2!=6×5×4×3×2×12×1×2×1×2×1=90通り )
重複順列(何回でも選べる)
名前は大げさですが、一番単純な順列です。
基本的考え方
例えばサイコロを3回振る場合の目の出方を考えると、63=216通り ですね。
順列の最初に出てくる例の「1~6のカードから3枚選んで3桁の整数を作る」場合は一度使った数(カード)は使えませんが、サイコロを降る場合は同じ数を使えるのが異なります。これを「重複順列」と呼んでいるだけです。
n種類あるものをr個選んで並び替える
→nr 通り
(例)サイコロを3回振る→63 通り
数以外にも、モノ(人)の振り分けにも使います。
(例1)区別があるAB2つの箱に色の違う5個の玉を分ける(0個の箱があってもOK)
→手順①箱の名前ABを書いたシールをランダムに選んで玉に貼っていきます。
手順②貼り終わったらシールに書いてある名前の箱に入れます。
手順①が重複順列で、25=32通り です。
この問題では「0個の箱があってもよい」と注意書きがあって、例えば5個の玉全部に「A」のシールが貼られた場合は5個の玉全部がAの箱に入り、Bの箱は空になってしまいますが、それでもOKという意味です。
(例2)ABCD4人に、3種類のアイスから選んで配る(選ばれない種類があっても良い)
→手順①アイスの種類を書いた紙をランダムに選んで4人に渡します。
手順②渡し終わったら紙に書いてある種類のアイスを配ります。
手順①が重複順列で、
34=81通り[/su_spoiler]
応用
先程の例題1
区別があるAB2箱に色の違う5個の玉を分ける(0個の箱があってもOK)が「0個の箱(空箱)があるとダメ」となっている場合があります。
その場合、先程の答え 25=32通り から「空箱がある」場合を引かないといけません。
空箱があるのは、箱ABどちらか5個の玉全部が入る場合なので 2通り です。
結局、32–2=30通り が答えになります。
先程の例題2
ABCD4人に、3種類のアイスから選んで配る(選ばれない種類があっても良い)が「選ばれない種類のアイスがあるとダメ」となっている場合は、選ばれない種類があっても良い単純な場合の35=243からダメな場合を引きますが、計算が少し複雑になります。
ダメな場合は更に細かく分けると「5人全員に1種類のアイスが配られた場合X」と「5人に2種類のアイスしか配られていない場合Y」の2つあります。
Xは3種類のアイスから1種類を選ぶので、3C1=3通りです。
Yはまず、選ばれないアイスの種類の選び方が3C1=3通りあります。次に5人への2種類のアイスの配り方は例題1と同じ考え方ができます。25=32通りから、全員が同じ種類のアイスを配られる場合(2種類から1種類を選ぶ)2通りを引いて、25-2=30通りです。合計でYは 3×30=90通り です。
これでダメな場合が全部でX3+Y90=93通り と分かりました。
以上より243–93=150通りが答えになります(面倒くさかったですね…)
→詳しくは「組分け問題の解法全8パターン」のパターンAを見て下さい。
重複組み合わせ
基本
n種類あるものをr個選ぶ。例えばabc3種類のジュースを自由に組み合わせて5本買う(選ばない種類があっても良い)ような場合です(n=3,r=5)。
手順を分解してみるとこうなります。
➀ジュース一本が入るケースを横に5個並べます。次に仕切り板を2枚用意します。この5+2=7個のモノを自由に並び替えます(仕切り板が端に来ても良いし、仕切り板が2枚並んでも良い)。
すると5個のケースは「左の仕切り板よりも左(A)」「二枚の仕切り板の間(B)」「右の仕切り板よりも右(C)」の3つのグループABCに分けられます(図1)。
➁そしてAにあるケースにはaジュース、Bにあるケースにはbジュース、Cにあるケースにはcジュースを入れます。(図2)
仕切り板が端に来るとAやCのグループが無くなり、仕切り板が隣り合った場合はBグループが無くなります(図3)が、今回はOKです。
((図2))((図3))
手順➀は5個のケースと2枚の仕切り板を並べるので、同じものが2個、5個ある合計7個の並べ替えなので、xxxxxとyyを並べ替えるアルファベット順列と同じになり、
7!2!×5!=21通り です。
このようにn種類あるものをr個選ぶ場合は、(n-1)個の仕切りと区別が無いr個のものを並べ替えるので同じものを含む順列(アルファベット順列)と同じ公式になる。
nHr={(n-1)+r}!(n-1)!×r!
多くのテキストとは違うと思いますが、コチラのほうが自然で分かりやすいはずです。
(同じように考える問題)
3つの箱abcに区別の無い5個の玉を入れる(空の箱があっても良い)
応用
空の箱や選ばれない種類が許されない場合は、全く違った考え方になります(覚えておかないとキツいです)。
例えば、abc3種類のジュースを自由に組み合わせて5本買う(どの種類も最低1本は選ぶこと)場合です。手順はこうなります。
➀ジュース一本が入るケースを横に5個並べます。次に仕切り板を2枚用意して、ケースの間に一枚ずつ入れます。
すると5個のケースは「左の仕切り板よりも左(A)」「二枚の仕切り板の間(B)」「右の仕切り板よりも右(C)」の3つのグループABCに分けられて、ABCのグループに必ず1個はケースが存在するはずです(図1)。
➁そしてAにあるケースにはaジュース、Bにあるケースにはbジュース、Cにあるケースにはcジュースを入れます。(図2)今回はどのジュースも必ず1本は選ばれます。
((図))
手順➀は5個のケースの間 5-1=4個 から2個を選んで仕切り板を入れるので、4個から2個を選ぶ組み合わせになり
4C2=4×32×1=6通りが答えになります。
(同じように考える例)3つの箱abcに5個の玉を入れる(空の箱があってはいけない)
色んな考え方が出てきて頭が混乱しますね…
玉や人を分ける問題については「組分け問題のまとめ」に整理してあるので参考にして下さい。
組分け問題
(分け方の人数指定がない場合)
分け方の人数指定がある場合は「場合の数の基本と利用」のコチラで扱いましたが、分け方の人数指定が無い場合はここまでに学習した定理・公式を総動員して解きます。
詳しくは「組分け問題全8パターンの解き方」を見て下さい。
次のステップへ
場合の数の応用公式は分かりましたか?分かった人は場合の数の総仕上げ「組分け問題」や確率に進んで下さい。
最後まで読んでいただきありがとうございました。この記事があなたの役に立てたなら嬉しいです♪