●総まとめ(このページ)
○場合の数の2つの公式と使い方
○いろいろな順列と組み合わせ
○組分け問題
○二項定理・三項定理
○確率の基本
○いろいろな確率
○独立試行と反復試行
○期待値
「定期テストで場合の数・確率が出るけど、全然分かんない!」という高校生の皆さんへ。数式に惑わされず具体例で考えれば分かりますよ!東大卒講師歴20年の管理人がまとめました。確認テストがあるので定着するまで繰り返し練習してみましょう。
目次(クリックでジャンプ)
場合の数(基本)
場合の数え方には「順列」と「組み合わせ」がある。
順列
いくつかの中から選んで並べ替える(順番のある枠に入れる)
●n個からr個選んで並べる nPr
(例)5個から3個選んで並び替える
→ 5P3=5×4×3=60
(例)10個から4個選んで並び替える
→10P4=10×9×8×7=5040
●n個を並び替える r! (階乗)
(例)3個を並び替える→3!=3×2×1=6
(例)5個を並び替える→5!=5×4×3×2×1=120
確認テストをどうぞ
8人からリレー選手の一番手二番手アンカー3人選ぶ。
→( 8P3=8×7×6=336通り )
1から9までの数字から4つ選んで4ケタの整数を作る。
→( 9P4=9×8×7×6=3024通り )
4人が横一列に並んで記念撮影するときの並び方
→( 4!=4×3×2×1=24通り )
詳しい説明を読みたい人は「場合の数の基本と利用」内のコチラを見て下さい
組み合わせ(nCr)
いくつかの中から選ぶ(だけ)が「組み合わせ」
●n個からr個選ぶ nCr=nPr÷r!
(例)7C2=7×62×1=21通り
(例)10C3=10×9×83×2×1=120通り
●nCr=nCn-r
(例)10C7=10C10-7=10C3
考え方
「組み合わせC」は「順列nPr」に比べると、r! 個の場合を重複カウントしているので、nPrをr!で割ります。
また「10個から9個を選ぶ」のは「10個のうち選ばない1個を選ぶ」のと同じなので10C9=10C10-9=10C1 というふうに計算を簡単にできます。
確認テスト
10人から代表4人を選ぶ
→( 10C4=10×9×8×74×3×2×1=210通り )
1から9までの数のうち好きな数を5つえらぶ
→( 9C5=9×8×7×6×55×4×3×2×1=126通り
9C5=9C9-5=9C4 で計算すると少しラク )
20人から16人を選ぶ
→( 20C16=20C20-16=20C4
=20×19×18×174×3×2×1=4845通り )
詳しい説明を読みたい人は「場合の数の基本と利用」内の「順列」を見て下さい
公式の利用(人数指定のある組分け)
考え方
「◎人を◎部屋に●人ずつ分ける」というような人数指定のある組分け問題はnCrの積になる。
(例)「4人の生徒を部屋Aに2人、部屋Bに2人と分ける」
→ 4C2 × 4-2C2= 4C2 × 2C2 =4×32×1×1=6通り。
さらに、部屋に区別が無い場合は、nCrの積を人数が同じ部屋の数の階乗で割る。
(例)「4人の生徒を2つの部屋に2人ずつ分ける(同じ2人部屋が2つ)」
→ 4C2 × 2C2 ÷2!=4×32×1×1÷2=3通り。
確認テストにトライ♪
6人の生徒をABC3つの部屋に2人づつ分ける場合
→( 6C2×4C2×2C2=6×52×1×4×32×1×2×12×1=90通り )
6人の生徒を区別の無い3つの部屋に2人づつ分ける場合
→確認テスト1を( 3! :人数が同じ部屋が3つ )で割る
→( 6C2×4C2×2C2÷3!=6×52×1×4×32×1×2×12×1÷(3×2×1)=15通り )
5人の生徒を部屋Aに2人、Bに2人、Cに1人分ける場合
→( 5C2×3C2×1C1==5×42×1×3×22×1×1=30通り )
5人の生徒を区別のない3つの部屋に2人、2人、1人と分ける場合
→確認テスト3を( 2! :人数が同じ部屋が2つ )で割る
→( 5C2×3C2×1C1÷2!=5×42×1×3×22×1×1÷(2×1)=15通り )
6人の生徒を部屋Aに3人、Bに2人、Cに1人分ける場合
→( 6C3×3C2×1C1=6×5×43×2×1×3×22×1×1=60通り )
6人の生徒を区別のない3つの部屋に3人、2人、1人と分ける場合
→確認テスト5を( 割る必要は無い(人数が同じ部屋がないから) )
→( 6C3×3C2×1C1=6×5×43×2×1×3×22×1×1=60通り )
詳しい説明を読みたい人は「場合の数の基本と利用」内の「組み合わせ」を見て下さい。
場合の数の公式(応用)
円順列
●n個からr個選んで円に並べる
→ nPr÷r 通り
○r個を円に並べる
→ (r-1)! 通り
○数珠順列(反対向きも同じに数える)
→ 円順列÷2 =nPr÷r÷2 通り
→ r個を円に並べる時は (r-1)!÷2 通り
円形にr個並べると同じ形がr個できて重複カウントしていることになるので、順列nPrをrで割る。
n人全員を円形に並べる時は、階乗n!をnで割る
また、裏返したものも同じと数える(数珠順列)場合、重複カウントが2倍になるので、円順列を÷2する。
7人から4人選んで丸テーブルに座らせる
→( 7P4÷4=7×6×5×44=7×6×5=210通り )
7人全員を丸テーブルに座らせる
→( (7-1)!=6×5×4×3×2×1=720通り )
応用問題(場所の指定)
ABCDEFの6人が円に並ぶ場合、AとBが向かい合うのは何通りあるか
→AとBを向かいに座らせる(AとBを固定)のは( 1 )通り
→残った4席にCDEFを座らせるのは( 4!=24通り(円順列ではない) )
→答えは( 1×24=24通り )
男子ABC女子XYZ合計6人が円に並ぶ場合、男女が交互に並ぶのは何通りあるか?
→男子ABC3人を円に並べるのは( (3-1)!=2通り )
→次にそのスキマ3箇所に女子を並べるのは( (円順列ではない) 3!=6通り )
→答えは( 2×6=12通り )
詳しい説明が見たい人は「場合の数の応用」内のコチラをどうぞ。
同じものを含む順列
「アルファベット順列」
同じ種類のものp個q個…を含む合計x個のものを並べ替える
→x!p!×q!… 通り
同じ種類の個数の階乗(!)ずつ重複カウントがあるので、順列nPrを重複カウントp!q!で割る。
aを3個bを2個含む合計6個の「a,a,a,b,b,c」を並び替えて単語を作る
→( 6!3!×2!=6×5×4×3×2×13×2×1×2×1=60通り )
詳しい説明が見たい人は「場合の数の応用」内の「アルファベット順列」をどうぞ。
重複順列(何回でも選べる)
n種類あるものをr個選んで並び替える
→nr 通り
(例)サイコロを3回振る→63 通り
サイコロを降るように同じ数を使える場合や、区別があるモノ(人)を区別のある場所に振り分けるのに使う。
区別がある3箱に色の違う5個の玉を分ける(0個の箱があってもOK)
→( 35=243通り )
ABCDEF6人に、2種類のアイスXYZから自由に選んで配る(選ばれない種類があっても良い)
→( 26=64通り )
応用
もし、「0個の箱があるとダメ」とか「選ばれない種類があったらだめ」という場合は、空箱がある場合を求めて、nr から引いて答えを出します。
(例)区別があるAB2箱に色の違う5個の玉を分ける(0個の箱があったらダメ)
→0個の箱があっても良い場合の答え 25=32通り から「空箱がある」場合=箱ABどちらか5個の玉全部が入る場合なので 2通り を引いて 32–2=30通り が答え
詳しい説明が見たい人は「場合の数の応用」内の「重複順列の応用問題」をどうぞ。
重複組み合わせ(nHr)
n種類あるものをr個選ぶ
→nHr={(n-1)+r}!(n-1)!×r!
(例)abc3種類のジュースを組み合わせて5本買う
→{(3-1)+5}!(3-1)!×5!=7!2!×5!=21
n種類あるものをr個選ぶ場合はアルファベット順列の応用になります。
(例)abc3種類のジュースを自由に組み合わせて5本買う場合(n=3,r=5)。
→「ジュースを入れる5個のケースと2枚の仕切り板(3つの場所に仕切るので2枚で足りる)を並べかえ」と考えると、xxxxxとyyを並べ替えるアルファベット順列と同じで、
7!2!×5!=21通り です。
3種類の場合に仕切りが(3-1)=2個になるのに注意しましょう。
(多くのテキストとは違うと思いますが、コチラのほうが自然で分かりやすいはず)
4つの箱abcdに区別の無い10個の玉を入れる(空の箱があっても良い)
→( 4種類のモノを10個買うのと同じ。仕切りの数は4-1=3個 )
→( (3+10)!3!×10!=13!3×10!=13×12×113=572通り )
応用
空の箱や選ばれない種類が許されない場合は単純な組み合わせの問題に変わります。
(例)abc3種類のジュースを自由に組み合わせて5本買う(どの種類も最低1本は選ぶこと)
→5個のケースの間 5-1=4個 から2個を選んで仕切り板を入れるので、4個から2個を選ぶ組み合わせになり
4C2=4×32×1=6通り
詳しい説明が見たい人は「場合の数の応用」内の「重複組み合わせの応用」をどうぞ。
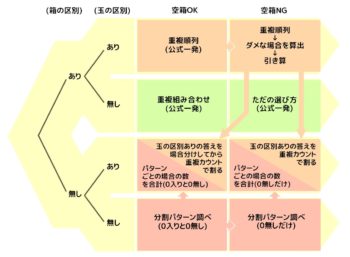
場合の数の総仕上げ(組分け問題)
人やモノを部屋や箱に分ける時に人数・個数の指定が無い問題で、場合の数の「総仕上げ」です。
❶部屋(箱)の区別の有る無し ❷モノ(人、玉)の区別の有る無し この2つの基準で4パターンに分けて、さらに❸空き部屋(箱)がダメな場合をプラスして全部で8パターンに分けて考えます。
詳しくは「組分け問題全8パターンの解き方」を見て下さい。
二項定理
●二項定理
p+q=nのとき、(a+b)nのapbqの係数はnCq (または nCp)
(例)(x+y)7のx2y5の係数は
●三項定理
p+q+r=nのとき、(a+b+c)nのapbqcrの係数はn!p!q!r!
(例)(x+y+z)7のx2y3z2の係数は
二項定理
(x+y)3を展開した時の「x2y」の係数はいくつかというと、公式「(x+y)3=x3+3x2y+3xy2+y3」を思い出せば「3」と分かります。
しかし (x+y)10を展開した時の「x2y8」の係数はいくつになるかは公式を覚えていないし実際に展開するのは面倒くさいですね。これを簡単な計算で求めるのが二項定理です。
定理を導く
(x+y)3を展開した時の「x2y」の係数がどう決まるか考えてみます。
(x+y)3=(x+y)(x+y)(x+y)なので、これを展開してできる項は、3つの(x+y)からxかyのどちらかを選んでかけたもので、
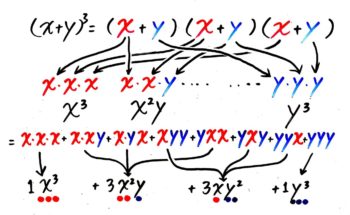
これは「x」「y」と書かれた2つの玉が入った3つの箱から玉を1つづつ合計3つ取り出すようなものです。

そして「x2y」の項は2つの箱からx玉を、1つの箱からy玉を取り出しているので、その取り出し方は3つの箱からxを取り出す2つの箱を選ぶ(または3つの箱からyを取り出す1つの箱を選ぶ)場合の数(組み合わせ)の「3C2」(または「3C1」)=3通りで、係数は3と分かるのです。
要するに、(x+y)3を展開した時の「x2y(1)」の係数は3C2(または3C1)ということです。この時、xとyの累乗の数は勝手に決められず、和が3になっているのも分かります。
この理屈を使って、(x+y)10を展開した時の「x2y8」の係数を求めると、10C2(または10C8)=10×92×1=45と分かります!
(展開で出すかと思うと気が遠くなりますねw)
これを定理の形にしたのが二項定理です。
p+q=nのとき、(a+b)nのapbqの係数はnCq (または nCp)
(理由)n個の(a+b)からaかbを選ぶときに、bをq個(またはaをp個)選ぶ組み合わせの数がnCq(nCp)だから
(例)(x+y)10のx2y8の係数は10C
別の考え方(この後使います)
教科書には上記の考え方が書いてありますが、もっと単純に次のように考えてもよいでしょう。
「x2y」になる項を展開直後の(降べき順の並べ替えをしていない)形で書くと「xxy」「xyx」「yxx」の3通りで、これが係数3になっています。
そしてこれは「x,x,y」の並び替えなので「同じもの2つ(と1つ)を含む合計3個を並び替えるアルファベット順列」の公式で3!2!×1!=3×2×12×1×1=3 と分かります。
練習問題
(x+y)7を展開したときにx5y2の係数はいくつか?
→( n=7,p=5,q=2 なので、nCp=nCq=7C2=21 )
(2x+3y)7を展開した時のx5y2の係数はいくつか?
注意:単純な nCp=nCqで終わりではない
→( 二項定理で出るのは(2x)5(3y)2 の係数 )
→( 二項定理を計算すると7C5=7C2=21 )
→( 21(2x)5(3y)2 になるので、これを整理して21×32x5×9y2=6048x5y2)
→( 答えは6048 )
三項定理
三項式の累乗、例えば(x+y+z)9を展開した時の「x2y3z4」の係数はいくつになるかを求めるのが三項定理です。
定理を導く
二項定理の「もう一つの考え方」を使えば簡単です。
「x2y3z4」になる項は「x,x,y,y,y,z,z,z,z」の並び替えなので「同じもの2つと3つと4つを含む合計9個を並び替えるアルファベット順列」で9!2!×3!×4!=1260通り と分かります。
これを定理にしたのが三項定理です。
p+q+r=nのとき、(a+b+c)nのapbqcrの係数はn!p!q!r!
(理由) aをp個,bをq個,cをr個含む合計n個の並べ替え(アルファベット順列)だから
(例)(x+y+z)9のx2y3z4の係数はで9!2!×3!×4!=1260通り
練習問題
確率
試行と事象
確率と基本性質
確率
ある条件を満たす確率=条件を満たす場合の数すべての場合の数
余事象の確率
条件を満たす確率=1ー余事象の確率
余事象=条件を満たさない場合 で、「条件を満たす場合=すべての場合-余事象」と言い換えることができます。
ところで、条件を満たす場合の方が圧倒的に多い問題では条件を満たさない場合(余事象)を求めるほうが簡単です。
例えば「10枚のコインを振って、少なくとも1枚は表になっている確率」を求める場合は、「少なくとも1枚は表になっている場合」を真正面から求めるよりも余事象(条件を満たさない場合)つまり「すべてのコインが裏の場合」を求めるのがラクですね(1通りですw)。
そして最初に書いた「条件を満たす場合=すべての場合ー余事象(条件を満たさない場合)」なので、この等式を「すべての場合」で割ると確率になります。
「条件を満たす場合すべての場合=すべての場合すべての場合ー余事象(条件を満たさない場合)すべての場合」で言い換えると
「条件を満たす確率=1ー余事象の確率」
先程の問題の場合、すべての場合が210=1024通り、余事象が1通り で余事象の確率が11024なので、条件を満たす確率=1-11024=10231024 と分かります。
確認問題(2020.1.16作成中)
確率の和(加法定理)AまたはB
確率の積(乗法定理)AかつB
和事象の確率
独立試行の確率
「独立」の意味
普通は「玉を取り出し」たり「くじを引いたり」したら玉やクジを戻さないので、二回目の玉取り出しやクジ引きの確率は一回目の結果に左右されます。
それに対して、取り出した玉やくじを戻すと、二回目の玉取りやくじ引きの結果は一回目の結果にまったく影響されません。これを「他の試行から独立している」と言います。
問題を解く時は「分母が常に等しい」のが特徴になります。
他の試行の結果に全く影響されないこと
反復試行の確率
独立したn回の試行で「当たり(確率P)」がr回出る確率
=nCr×Pr×(1-P)(n-r)
(例)サイコロを3回振って1の目が1回だけ出る確率
→3×(16)1(56)2 =2572
反復試行の例と結果
例えば「サイコロを3回振って1の目が1回だけ出る確率」のように、独立した試行を反復する場合に「当たり(この場合確率16)」が何回か(この場合1回)出る確率です。
まず、3回振って1の目が1回だけ出るような「出方のパターン」を調べます。当たりを「O」ハズレを「X」とすると、条件を満たすパターンは「OXX」「XOX」「XXO」の3つあります。
この3つのパターン(ABCとします)の確率を出して合計すれば(確率の加法定理)答えになります。
まずパターンAです。「O」の確率は16「X」の確率は(1-16)=56なので、パターンA(OXX)の確率は(16)×(56)×(56)=(16)1(56)2になります。
次に、パターンB(XOX)の確率は(56)×(16)×(56)=(16)1(56)2 で、これはAと等しいです!
そしてC(XXO)の確率も(16)×(56)×(56)=(16)1(56)2 と等しいです。
よってABCの確率を合計すると、(16)1(56)2+(16)1(56)2+(16)1(56)2=3×(16)1(56)2 =2572と分かりります。
定理を導く
上で求めた式 3×(16)1(56)2 は
❶当たりのパターン数(ここでは3)
❷(当たる確率)(当たる回数)(ここでは(16)1)
❸(当たらない確率)(当たらない回数)(ここでは(56)2)
の3つのかけ算です。これを分かりやすい日本語にすると、
何回か引いてそのうち何回か当たる確率
=(当たりのパターン数)×(当たる確率)(当たる回数)×(当たらない確率)(当たらない回数) という公式ができますね。
これを数学の語句に直すと、教科書の公式が出来ます。
まず「n回引いてr回当たるパターン数」は「n回のうち当たるr回を選ぶ場合の数」なので「nCr」です。
次に、当たる確率をPとすると、ハズレの確率は(1-P)になります。
また当たる回数はr回なので、ハズレの回数は(n-r)になります。
以上をまとめると、反復試行の確率=nCr×Pr×(1-P)(n-r) になります。この式を覚えるというよりも、問題文から具体的な式を作れればOKです。
練習問題
サイコロを5回振って3の倍数が2回だけ出る確率は?
→三つの部分を出してかけ算します。
❶当たりのパターン数は( 5回から3回当たりの回を選ぶので5C3=5C2=5×42×1=10通り)。
❷当たる確率(3の目か6の目が出る)が( 26=13 )で、当たりの回数が( 2回 )
❸ハズレの確率が( 1-13=23 )で、ハズレの回数が( 5-2=3回 )。
→5回中2回3の倍数が出る確率は( 10×(13)2×(23)3=10×2335=80243 )
反復試行の問題は、様々な条件とセットで出されることが多いです。
サイコロの出目で動く点
ゲーム
条件付き確率
例えば、10人の生徒に対して2問のクイズを出したとします。第一問を正解した人が6人、第二問を正解した人が5人、両方正解した人が3人がいた時に、次の確率を求めます。
①第一問を正解する確率→6人10人中=35ですね。
②第二問を正解する確率→5人10人中=12ですね。
③第一問も第二問も正解する確率→3人10人中ですね。
では「第一問を正解した人が第二問を正解する確率」はいくつでしょうか?
これは③とは違うことに注意しましょう。「第一問を正解した人が」という条件がついているので、直感的に両方正解した人第一問を正解した人のうち=3人6人中=12かな?という気がしますよね?答えとしてはそれで正解です。
ここで、約分する前の分数の分母と分子両方に10を分子として付けて、
310 610
にすると、分母が①の答え(10人中6人)で分子が③の答え(10人中3人)になっているのが分かります。これが「条件付き確率」の公式です。
まとめると、二つの条件がある時に、第一・第二条件をともに満たす確率第一条件を満たす確率が「条件付き確率」になります。
数学用語で書くとこうなります。
条件付き確率PA(B)=P(A∩B)P(A)
確率の乗法定理
条件付き確率の公式の分母を払う(両辺にP(A)をかける)と
P(A∩B)=P(A)×PA(B) となります。これが確率の乗法定理です。
分かりやすく日本語にすると、
「二つの条件を満たす確率」=「第一条件を満たす確率」×「条件付きで第二条件を満たす確率」
になります。まあアタリマエの日本語ですが…
期待値
あなたの友達があつめて「宝くじ」を企画しました。全部で10本のくじがあって、10000円の1等賞が1本、1000円の2等賞が3本、100円の3等賞が7本入っていて、くじの券が1枚1500円です。友達は「1等が1万円だし、よほど運が悪く無い限り1000円は当たるから、絶対にオトクだよ。不安なら2本・3本と買えば1等も当たりやすくなるし!」とうるさく誘ってきます。このくじを買うべきでしょうか?これを数学的に判断できるのが期待値です。
定理を導く。
1等は10000円と高額ですが当たる確率が110しかないので、この1等賞の存在からは、10000×110=1000円しか期待できないと考えます。
同じように2等は1000円で当たる確率が310なので1000×310=300円を、3等は100円で当たる確率が710なので100×710=70円を期待できます。以上を合計した1000+300+70=1370円がこのくじに期待できる合計金額です。
さて、このくじの購入価格は1500円でした…これは今計算した金額1370円を上回っていますから、このくじは「やや買い損」と評価できます。(といっても、かなり良心的なくじなので、お楽しみとして買ってあげるのもよいでしょう)
このように、変化する数量(この場合賞金)と対応する確率をかけたものの合計を「期待値」と言います。
期待値=(変化する量1×その確率)+…+(変化する量~×その確率)
(例)10000円の1等賞が1本、1000円の2等賞が3本、100円の3等賞が7本入っている10本のくじの期待値
→(10000×110)+(1000×310)+(100×710)
=1000+300+70=1370円
練習問題
1等10000円が一本、2等1000円が3本、3等100円が50本入った全部で100本の宝くじの期待値は?
→( (10000×1100)+(1000×3100)+(100×50100)
=100+30+50=180円 )
終わりに
場合の数と確率の全体像はつかめたでしょうか?大丈夫!という人はあとは演習あるのみ。
最後まで読んでいただきありがとうございました。この記事があなたの役に立てたなら嬉しいです♪