分かりやすい♪対数(log)の意味・公式まとめ。対数表の使い方も

「対数って何？」「ログって良く分からない…」という高校生の方へ。確かに日常生活であまり耳にしない言葉なので難しく思えるかもしれません。でも「指数」が分かれば対数も分かりますよ！この記事は東大卒講師歴20年の管理人が対数(log)(ログ)の意味を分かりやすく説明します。

対数の基本

対数は指数の○

「対数」を一言で言うと、「指数の逆」です。だから指数を思い出しましょう。指数法則「a^k=N」を日本語に直すと「aをk乗するとNになる」ですね。

この言葉の順序を変えてｋを求めるようにすると「aをNにするにはk乗すればよい」になります。

この「aをNにするにはk乗すれば良い」を数式にしたのが log_aN=k で「ろぐえいえぬいこーるけい」と読みます。

対数(log)の意味

「log_aN」→aを何乗すればNになるか？
「log_aN=k 」⇔「 a^k=N」
(aをNにするにはｋ乗する)　(aをk乗するとNになる)

(例)「log₃9=2 」⇔「 3²=9」
(3を9にするには2乗する)　(3を2乗すると9になる)

指数法則に自信がない・忘れたという人は「指数法則の基本」「指数法則の拡張」をよく見直して下さい。

対数の構成要素

log全体を「対数」と呼びます。

「log_aN」のNを真数と呼びます。Nには「0<N」という条件があります。(真数条件と言います)

「log_aN」のaを底と呼びます。aにも条件があり、「0<a」というのはNと同じですが,さらに「a≠1」という条件があります(１は何乗しても1にしかなりませんね)。

全部合わせると「log_aN=k」は「aを底とするNの対数はk」という意味になります。

対数の要素

「log_aN＝ｋ」
a→底　N→真数　k=対数
(数字が3つある)
0<a,a≠1,0<N

指数⇔対数

指数から対数を作る練習

指数→対数

「 a^k=N」⇔「log_aN=k 」
(aをk乗するとNに)　(aをNにするにはｋ乗)

あまり難しく考えずに「●を○にするには◉乗すれば良い」という日本語を作り、その順に数字を並べて「log●○＝◉」という式を作りましょう。そのうちに意味も実感できるようになります。

例1

3²=9　を logaN=k の形にせよ

解説と解答を表示

→「3を2乗すると9になる」
→「3を9にするには2乗すれば良い」
→log₃9=2　

例2

2^-3=
18を logaN=k の形にせよ

解説と解答を表示

→「2を-3乗すると18になる」
→「2を18にするには-3乗すれば良い」
→log218=-3　

例3

5^{$\frac{1}{2}$}=$\sqrt{5}$ を logaN=k の形にせよ

解説と解答を表示

→「5を12乗すると25になる」
→「5を$\sqrt{5}$にするには12乗すれば良い」→log5$\sqrt{5}$=12

対数から指数を作る

対数→指数

「log_aN=k 」⇔「 a^k=N」
(aをNにするにはｋ乗)　(aをk乗するとNに)

(例1)log₂32=5 を「a^k=N」の形に直せ

解説と解答を表示

「2を32にするには5乗すればよい」
→「2を5乗すると32になる」
→2⁵=32

(例2)log₄4=1 を「a^k=N」の形に直せ

解説と解答を表示

「4を4にするには1乗すればよい」
→「4を1乗すると4になる」
→4¹=4

(例3)log_{$\frac{1}{2}$}16=－4 を「a^k=N」の形に直せ

解説と解答を表示

「12を16にするには－4乗すればよい」
→「12を－4乗すると16になる」
→(12)^-4=16

対数を求める

やり方(その1)

底が「2」「3」のような単純な数の場合
真数Nを「a^k 」の形になおした時の「ｋ」を答えるのが簡単でしょう。

対数を求める(1)

真数Nを底aの累乗a^kに変形
logaN＝logaa^k=k

例1

log232 を求めよ

解説と解答を表示

「log232=log22^?」と考えます
→「32＝2⁵」なので
→log232=log22⁵=5　

例2

log3181を求めよ

解説と解答を表示

→「3を何乗すると181になるか？」
→「181＝13⁴＝3^-4」
→log3181=log33^-4=-4　

例3

log3$\sqrt[3]{81}$ を求めよ

解説と解答を表示

→「3を何乗すると$\sqrt[3]{81}$になるか？」
→「$\sqrt[3]{81}$＝$\sqrt[3]{3^4}$＝$3^\frac{4}{3}$」
→log3$\sqrt[3]{81}$=log3$3^\frac{4}{3}$=43

例4*

log3$9\sqrt{3}$ を求めよ

解説と解答を表示

→「3を何乗すると$9\sqrt{3}$になるか？」
→「9×$\sqrt{3}$＝3²×$3^{\frac{1}{2}}$＝$3^{(2+\frac{1}{2})}$=$3^{\frac{5}{2}}$ なので
log3$9\sqrt{3}$=log3$3^{\frac{5}{2}}$=52

やり方(その2)*

底が単純な数でない場合(分数など)
対数「log_aN=k 」を指数「 a^k=N」の形に変形して指数方程式を利用する

対数を求める(2)

log_aN=X を a^x=N に変形して
指数方程式を解く

例5

log_{$\frac{1}{2}$}8 を求めよ

解説と解答を表示

log_{$\frac{1}{2}$}8=X ⇒ (12)^x=8
この指数方程式を解く

12=2^-1、8=2³なので、

(12)^x=8
↓
(2^-1)^X=2³
↓
2^-X=2³
↓
-X=3

ここからXの方程式

-X=3

↓
X=3÷(-1)=－3

例6

log_{$\frac{1}{4}$}$\sqrt{2}$ を求めよ

解説と解答を表示

log_{$\frac{1}{4}$}$\sqrt{2}$=X ⇒ (14)^x=$\sqrt{2}$
この指数方程式を解く

14=$2^{(-2)}$、$\sqrt{2}$=$2^{\frac{1}{2}}$なので、

(14)^x=$\sqrt{2}$
↓
$(2^{-2})^X$=$2^{\frac{1}{2}}$
↓
$2^{-2X}$=$2^{\frac{1}{2}}$
↓
-2X=12

ここからXの方程式

-2X=12

↓
X=12÷(-2)=－14

例7

log_{$\frac{1}{10}$}$\frac{1}{\sqrt{10}}$ を求めよ

解説と解答を表示

log_{$\frac{1}{10}$}$\frac{1}{\sqrt{10}}$=X ⇒ (110)^x=1$\sqrt{10}$
この指数方程式を解く

110=10^-1、1$\sqrt{10}$=10^{-\frac{1}{2}}$なので、

(110)^x=$\frac{1}{\sqrt{10}}$
↓
$(10^{-1})^X$=$10^{-\frac{1}{2}}$
↓
$10^{-X}$=$10^{-\frac{1}{2}}$
↓
-X=－12

ここからXの方程式

-X=－12

↓
X=－12÷(-1)=12

対数の性質と利用

基本ルール

log_aa^k=kこれは上にも出てきました。「aを何乗すればa^kになるか？→k乗」(a^k=a^k)

log_aa=1 「aを何乗すればaになるか？→1乗」(a¹=a)

log_a1=0 「aを何乗すれば1になるか？→0乗」(a⁰=1)

基本性質

log_aa^k=k
log_aa=1
log_a1=0

練習問題

対数をまとめる

❶和→積
logaM+logaN=log_aM×N (底が同じ対数の和は真数が積になる)

(証明)
log39+log327=log33²+log33³=2+3=5=log33⁵=log33³×3²=log39×27

❷差→除
logaM–logaN=log_aMN

(底が同じ対数の差は真数が除になる)

(証明)
log327－log39=log33³－log33²=3－2=1=log33¹=log33³÷3²=log327÷9=log₃279

多項をまとめる公式

(底aが等しい場合のみ)
❶logaM+logaN=logaMN
❷logaM-logaN=loga$\frac{M}{N}$

❸係数を中に入れる
ｋlog_aN＝log_aN^k(ログの係数は真数の指数になる)

係数を中に入れる

log_aN^k=ｋlog_aN

(証明)
log28²=log2(2³)²=log22⁶=6=2×3＝2×log22³＝2log28

例1

log39+log327 を計算しなさい

解説と解答を表示

log39+log327=log39×27=log33²×3³

=log33⁽²⁺³⁾=log33⁵=5

例2

log108+log10125 を計算しなさい

解説と解答を表示

log108+log10125=log108×125=log101000

=log1010³=3

例3

log₆19+log₆14 を計算しなさい。

解説と解答を表示

log₆19+log₆14=log₆19×log₆14=log₆136=log66^-2=－2

例4

log2160－log25 を計算しなさい

解説と解答を表示

log2160－log25=log₂1605=log232

=log22⁵=5

例5

log3$\sqrt{24}$－log3$\sqrt{8}$ を計算しなさい

解説と解答を表示

log3$\sqrt{24}$－log3$\sqrt{8}$=log3$\frac{\sqrt24}{\sqrt8}$
=log3$\sqrt{3}$=log3$3^{\frac{1}{2}}$=12

例6

log512－log5300 を計算しなさい

解説と解答を表示

log512－log5300=log512300=log5125=log55^-2=-2

対数をバラす

「まとめる」の逆方向

例1

log₁₀2=a、log₁₀3=b とするとき、次の値をa,bで表せ
(1)log₁₀120

(2)log₁₀0.15

新しい底の分数にする(底の変換公式)

対数の底とも真数とも違う新しい数字を底として、分数を作れます。他の対数と底を揃えるのに使います。

底の変換公式

log_aN=log_bNlog_ba

(証明)
(logaN=K)
↓
a^k=N
↓
logba^k=logbN
↓
klogba=logbN
↓
ｋ=$\frac{log{b}{N}}{log{b}{a}}$
↓
logaN=$\frac{log{b}{N}}{log{b}{a}}$

例題

対数関数

対数方程式・不等式

常用対数

10を底とする対数「log₁₀X」(10を何乗したらXになるか)を「常用対数」という。

(例)log₁₀100=(10を何乗したら100になるか)=2

(例)log₁₀10000=4

常用対数表の読み取り

今は「100」「10000」のように10を整数乗した数を例に出しましたが、「3」のような数はどうなるでしょう？

答えを言ってしまうと「log₁₀3」は「0.4771」になります。

つまり、「10」「100」以外のほとんどの数の常用対数は小数点のある中途半端な数になります。

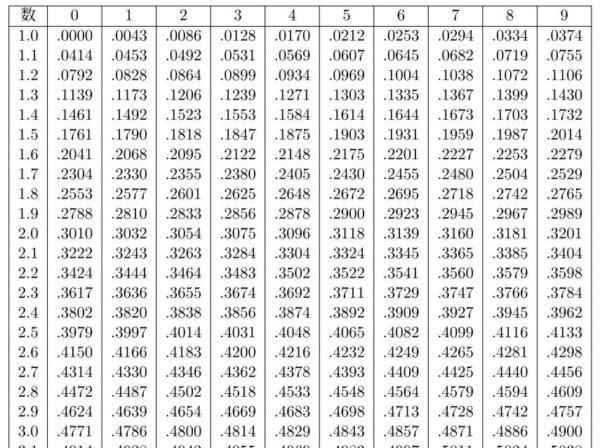
これらは暗算・筆算では簡単に出せないので「常用対数表」という表の形になったものを読み取って使います。

下にあるのは常用対数表の一部分を抜粋したものです。

常用対数表(一部)

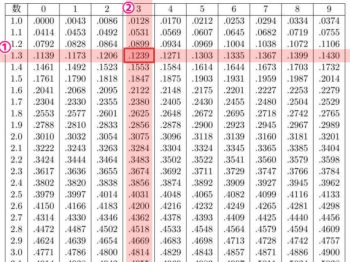
例えば「1.33の常用対数」「log₁₀1.33」(10を何乗すると1.33になるか)を読み取る場合

①まず左端のタテの列で「1.3」を探すと上から三行目に見つかります。
②次に小数第二位「3」を上端のヨコの列で探すと四列目にあるので、「1.3」の行の４列目をみると「.1239」とあります。

これが「1.33の常用対数」です。

1.33の常用対数を読み取る

常用対数表の読み取り

❶小数第一位までの数字でタテにたどる
❷小数第二位の数字でヨコにたどる

例1

2.46の常用対数(log₁₀2.46)を求めよ

解説と解答を表示

表で「2.4」の行と「6」の列をたどると0.3909と分かる

例2

常用対数が0.4594になる数(log₁₀X=0.4594 になるX)を求めよ

解説と解答を表示

今までと反対方向の作業をする。表の中から「0.4594」を見つけて行と列を読み取ると「2.8」と「8」なので、求める数Xは「2.88」と分かる。

常用対数表の利用

常用対数表にない数字でも、×10、×100、○10、○100などの形に変形すれば求めることができます。

大きな数の常用対数を求める

例えば、1330の常用対数つまり「log₁₀1330」を求める場合

1330=1.33×1000なので、log₁₀1330=log₁₀1.33×1000=log₁₀1.33+log₁₀1000 と変形できます。

log₁₀1.33は0.1239、log₁₀1000=log₁₀10³=3 なのでlog₁₀1.33+log₁₀1000=0.1239+3=3.1239 と分かります。

(例1)対数表を用いて log₁₀25.1 を求めよ

解説と解答を表示

25.1=2.51×10なので、log₁₀25.1=log₁₀2.51×10=log₁₀2.51+log₁₀10 と変形できます。
log₁₀2.51は0.1239、log₁₀1000=log₁₀10³=3 なのでlog₁₀1.33+log₁₀1000=0.1239+3=3.1239 と分かります

(例2)対数表を用いて log₁₀149 を求めよ

解説と解答を表示

小さい数の常用対数を求める

また0.133の常用対数つまり「log₁₀0.133」を求める場合は
0.133=1.3310なので、log₁₀0.133=log₁₀1.3310=log₁₀1.33－log₁₀10と変形できます。log₁₀1.33は対数表より0.1239、log₁₀10=log₁₀10¹=1 なので log₁₀1.33－log₁₀10=0.1239-1=–0.8761 と分かります。

(例3)対数表を用いて log₁₀0.0292 を求めよ

解説と解答を表示

0.0292=2.92100なので、log₁₀0.0292=log₁₀2.92100=log₁₀2.92－log₁₀100と変形できます。
log₁₀2.92は対数表より0.4654、log₁₀100=log₁₀10²=2 なのでlog₁₀2.92－log₁₀100=0.4654-2=–1.5346 と分かります。

対数表に無い数

●大きい数の常用対数
○「表の数値×10」→数値+1
○「　〃　 ×100」→　〃 +2
●小さい数の常用対数
○「表の数値10」→数値－1
○「表の数値100」→数値－2

整数部分のケタ数

例えば「50」の整数部分は「2」ケタです。この「50」という数からどうやって「2」が出てくるのでしょう。

ケタ数が変わるのは10,100,1000…で、50がどこにあるか考えると10と100の間(10<50<100)です。
10=10¹,100=10² なので、10<50<100→10¹<50<10² と直せます。
50の整数部分のケタ数「2」はこれだったのです。

つまり、ある数Xが10ⁿ<X<10ⁿ⁺¹ になる場合、Xは(n+1)ケタということです。

整数部分のケタ数

ある数Xが10ⁿ<X<10ⁿ⁺¹ である場合、
Xの整数部分は(n+1)ケタになる

では、「2⁵⁰」は何桁でしょうか。10ⁿ<2⁵⁰<10ⁿ⁺¹ となる場合、(n+1)ケタと分かるので、2⁵⁰=10^x としてxを求めます。(2を50回かけた結果の桁数を数えても良いですが…面倒くさいですね？)

2⁵⁰=10^x とすると、xは「10を2⁵⁰にするには何乗すれば良いか」なので、log₁₀2⁵⁰ です。

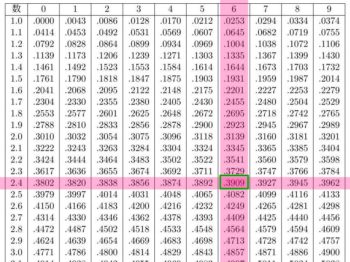
常用対数表でlog₁₀2を調べると、log₁₀2=0.3010 なので、log₁₀2⁵⁰

=50×log₁₀2=50×0.3010=15.05 と分かります。つまり2⁵⁰=10^15.05 です。

以上より 10ⁿ<2⁵⁰<10ⁿ⁺¹ → 10ⁿ<2⁵⁰=10^15.05<10ⁿ⁺¹ → 10¹⁵<2⁵⁰=10^15.05<10¹⁶ なので、2⁵⁰は16ケタと求められます!

(例)3¹⁰ の桁数を求めよ。log₁₀3=0.4771 とする

解説と解答を表示

3¹⁰=10^x とすると、x=log₁₀3¹⁰

log₁₀3¹⁰=10×log₁₀3=10×0.4771=4.771 と分かります。つまり3¹⁰=10^4.771 です。

以上より 10ⁿ<3¹⁰<10ⁿ⁺¹ → 10ⁿ<3¹⁰=10^4.771<10ⁿ⁺¹ → 10⁴<3⁴⁰=10^4.771<10⁵ なので、3¹⁰は5ケタ

(例)3⁴⁰ の桁数を求めよ。log₁₀3=0.4771 とする

解説と解答を表示

3⁴⁰=10^x とすると、x=log₁₀3⁴⁰

log₁₀3⁴⁰=40×log₁₀3=40×0.4771=19.084 と分かります。つまり3⁴⁰=10^19.084 です。

以上より 10ⁿ<3⁴⁰<10ⁿ⁺¹ → 10ⁿ<3⁴⁰=10^19.084<10ⁿ⁺¹ → 10¹⁹<3⁴⁰=10^19.084<10²⁰ なので、3⁴⁰は20ケタ

小数の数字部分

同じように、小数において0でない数字は小数第何位から現れるかを求めます。

例えば、「0.05」は小数第「2」位から0でない数字が現れます。

0.001<0.05<0.01

10^-3<0.05<10^-2

小数で数字が現れる位置

ある数Xが10^-(n+1)<X<10^-n である場合、
0以外の数字は小数(n)ケタになる