「弧度…って何?」「今までの度と何が違うの?」という高校生へ。東大卒講師歴20年の管理人が整理して図解します。記事を読み終われば頭がスッキリまとまっているでしょう。
目次(クリックでジャンプ)
弧度法(ラジアン)
今までの角度(0°,180°,360°等)=度数法
(「°」が付いている)
新しい角度の表し方(0,1$pi$,2$pi$)=弧度法
(「°」が付いていない)
◆弧度法の定義
$frac{l}{r}$=$theta$(ラジアン)

度数法と弧度法の変換
◆度数法と弧度法の対応
180°=1$pi$
これを頭に叩き込んで、あとは感覚で何となく解けるのがベスト!
度数法を弧度法に直す
❶度数法を180で割って
❷「°」を取り「$pi$」をつける。
もう少し感覚的に言うと、
「半円の何分のいくつか」をイメージして、
それに「$pi$」をつける感じです。
例題を解く前に…
公式をもう一回確認します。
言えるようにしてから例題に進んで下さい。
言えなかった人はもう一度閉じて、言ってみて下さい。
覚えたと思ったら、例題に進みましょう。
例題1
30°をラジアンに直せ
例題2
45°をラジアンに直せ
例題3
60°をラジアンに直せ
例題4
90°をラジアンに直せ
例題5
120°をラジアンに直せ
弧度法を度数法に直す
❶弧度法から「$pi$」をとって
❷180をかけて「°」をつける
これも、
言えるか確認してみましょう。
言えなかった人はもう一度閉じて、言ってみて下さい。
覚えたと思ったら、例題に進みましょう。
例題1
$frac{1}{6}$$pi$ を度数法で表わせ
例題2
$frac{1}{4}$$pi$ を度数法で表わせ
例題3
$frac{1}{3}$$pi$ を度数法で表わせ
例題4
$frac{1}{2}$$pi$ を度数法で表わせ
おうぎ形の計量
扇形の弧の長さ($l$)
一番最初の弧度法の定義
$frac{l}{r}$=$theta$(ラジアン)
こいつを変形して、$l$を出す。
$frac{l}{r}$=$theta$
↓(両辺に「r」をかける)
$l$=$theta$r

これも、
言えるか確認してみましょう。
言えなかった人はもう一度閉じて、言ってみて下さい。
覚えたと思ったら、例題に進みましょう。
例題1
半径3、中心角$frac{1}{4}$$pi$ の扇形の弧の長さを求めよ
例題2
半径8、中心角$frac{7}{12}$$pi$ の扇形の弧の長さを求めよ
例題3
半径6、中心角120° の扇形の弧の長さを求めよ
おうぎ形の面積(S)
扇形を三角形だと思って出す。
弧の長さ(l)が底辺で、半径(r)が高さ。
S=$l$×r×$frac{l}{2}$=$frac{1}{2}lr$
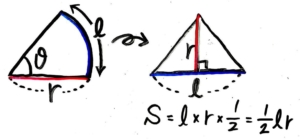
この式の$l$に$theta$rを代入して
S=$frac{1}{2}×l×r$=$frac{1}{2}×theta r×r$=$frac{1}{2}theta r^2$
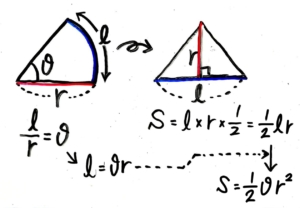
この図がかけるようにすると良い。
◆弧の長さ $l$=$theta$r
◆面積 S=$frac{1}{2}theta r^2$
これも、
言えるか確認してみましょう。
言えなかった人はもう一度閉じて、言ってみて下さい。
覚えたと思ったら、例題に進みましょう。
例題1
半径3、中心角$frac{1}{4}$$pi$ の扇形の面積を求めよ
例題2
半径8、中心角$frac{7}{12}$$pi$ の扇形の面積を求めよ
例題3
半径6、中心角120° の扇形の面積を求めよ
