「『人を部屋に分ける問題』が色々なパターンがあってややこしい!」「『組み分け問題』の解き方を整理したい!」という高校生の方へ。
この記事は「(人数を指定されない)組分け問題」の解法を東大卒で塾講師歴20年の管理人が分かりやすく図解します。記事を読めば頭の中がスッキリ整理されて、実際の問題を迷いなく処理できるようになりますよ!
「◎部屋に●人ずつ」と人数を指定される組み分け問題は別記事「場合の数の公式まとめ」内のコチラを御覧下さい。
目次(クリックでジャンプ)
組分け問題の考え方
こんにちは!受験図解講師の爽茶です♪
多くの本やWebが「組み分け問題」を分類・解説していますが、分類だけされても…実際に問題を解く時にどのやり方で解いたら良いのか、迷いが出てしまいますよね?
そこで当ブログでは分類だけでなく「組み分け問題」にあたった時の「考える手順」をお伝えします。
考える手順
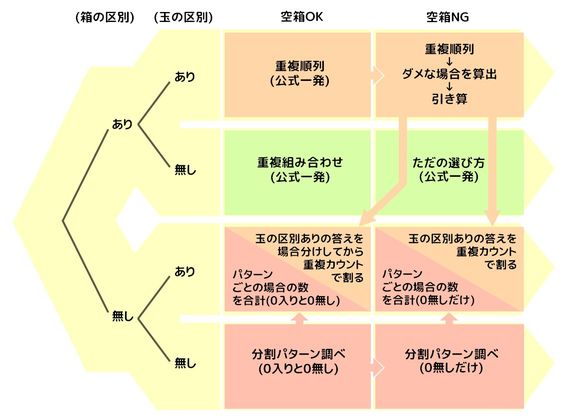
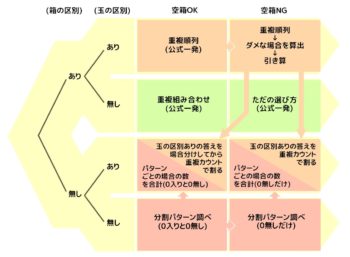
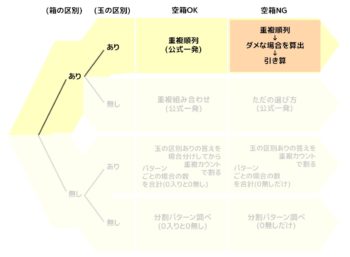
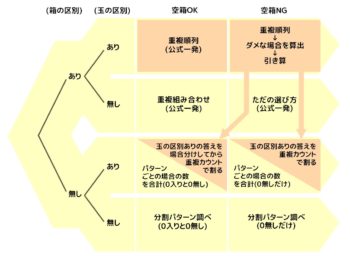
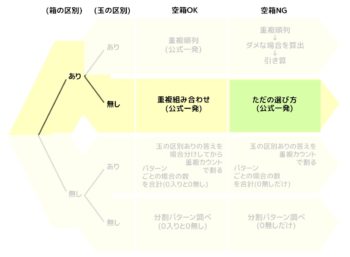
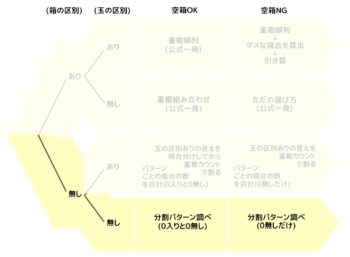
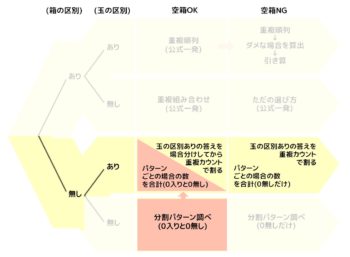
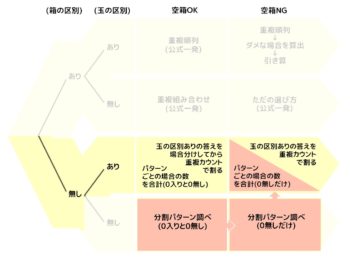
❶部屋(箱)の区別の有る無しで分ける
❷モノ(人、玉)の区別の有る無しで分ける
ここまででAからDまでの4パターンに分かれます。
❸空き部屋(箱)がダメな場合をプラス
これでA~Dそれぞれが2倍になって全部で8パターンになります
これを図にすると次のようになります。
全体像
樹形図風にしました。左上がA1、その右がA2、と右下のD2まで全8パターンで、C1とC2は解法が2つあります。
これをプリントアウトしたものを横において解法を読めば理解度がアップしますよ!
それでは次のような共通の例題をもとに8パターンを解いていきます。
5個の玉を3つの箱に分けます。全部で何通りありますか?
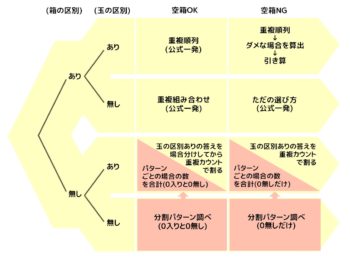
| 空きOK | 空きNG | |
| A:両方区別あり | 重複順列 | 重複順列ーダメな場合 |
| B:箱のみ区別あり | アルファベット順列 | ただの選び方 |
| C:玉のみ区別あり | A1の答えを重複カウントで割る | A2の答えを重複カウントで割る |
| D1の各場合を調べて合計 | D2の各場合を調べて合計 | |
| D:両方区別なし | 数字の分割 | 数字の分割 |
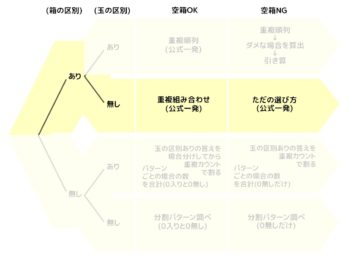
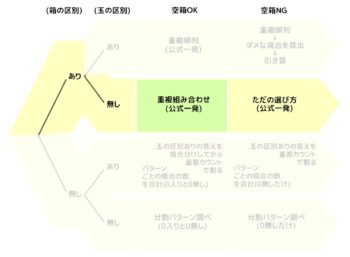
A:箱も玉も区別あり
はじめは箱も玉も区別がある場合です。
「生徒をABC三つの部屋に組分けする」などもこのパターンです。
A-1:空きOKの場合
→重複順列を使用:難易度★☆☆
色が違う5個の玉をA,B,C3つの箱に分けます。全部で何通りありますか?
「A」「B」「C」三種類のシールを5個の玉に貼っていくと考えます。すると、3つの目があるサイコロを5回ふるのと同じ(重複順列)なので、$3^5$になります。
$3^5$=3×3×3×3×3=243通り
A-2:空きNGの場合
→(A-1の答え)から(ダメな場合)を引く:難易度★★☆
色が違う5個の玉をA,B,C3つの箱に分けます。全部で何通りありますか?但し空き箱が無いようにします。
空きOKだった場合、重複順列で$3^5$=3×3×3×3×3=243通りでした。
ここからダメなもの(空き箱がある場合)を引けば答えになります。
ダメな場合①:5個の玉全部が1つの箱に入っている
→3つの箱から入っている箱を選ぶので3C1=3通り
ダメな場合②:5個の玉が2つの箱に入っている
→まず、空の箱の選び方が3C1=3通りあります。
次に、5個の玉を2箱に分けるのはさっきの重複順列の考え方(5個の玉それぞれに2種類のシールを貼る)の25=32通りから2つの箱のうちの1つの箱に入ってしまっている(5個の玉全部に同じシールが貼られている)2C1=2通りを引いて、25-2=30通りなので
合計で 3×30=90通り
つまりダメな場合が全部で➀3+➁90=93通り
以上より243–93=150通り
さて、この問題で求めた数値は、「C:玉だけ区別がある場合」で使うのでもう一度まとめておきます。
1つの箱に5個入っている:3通り
2つの箱に 〃 :90通り
3つの箱に分かれている:150通り
B:箱だけ区別あり
二番目は箱だけ区別がある場合で「3種類のジュースを合わせて5本買う」などもこのパターン(種類というワードに注目!)です。
独特な考え方を使いますが、計算は簡単な方です。
B-1:空きOK
→重複組み合わせ≒同じものを含む順列:難易度★★☆
5個の玉をA,B,C3つの箱に分けます。全部で何通りありますか?
これは同じ種類のものがあってもよい選び方で「重複組み合わせ」と言います。他の例では「オレンジ、グレープ、アップル3種類のジュースを合わせて5本買う」等があります。
この「重複組み合わせ」を単純化します。
5個の玉と2つの仕切りを細長い大きな箱にいれてシャッフルします。左の仕切りより左にある玉には「A」のシールを、2つの仕切りの間の玉には「B」のシールを、右の仕切りより右にあるたまには「C」のシールを貼ります。あとはシール通りに箱に入れていけば良いですね。3種類に分ける時は仕切りの数は2個になるのがポイントです。
((図))
これは、5個の玉と2個の仕切り合計7つの物体を並べ替える順列で、アルファベット「a,a,a,a,a,b,b」を並べ替えて単語を作る「同じものを含む順列(アルファベット順列)」と同じです。
「同じものを含む順列」の公式にしたがって、
(5+2)!5!×2!=7!5!×2!=7×6×5×4×3×2×15×4×3×2×1×2×1=7×62×1=7×31=21通り
B-2:空きNGの場合
→単純な選び方(組み合わせ):難易度★☆☆
5個の玉をA,B,C3つの箱に分けます。全部で何通りありますか?但し空き箱が無いようにします。
これも「仕切り」の考え方を使いますが、今度は空き箱がダメ=「A」「B」「C」のシールが1枚は貼られていないといけません。これは、仕切りが端になったり仕切りが隣り合ったりしてはダメということです。
そこでまず箱に玉を入れてしまいます。
((図))
この状態で玉と玉の4つのすき間のうちどこか2箇所に1つづつ仕切りを差せば、A,B,C3箇所に分けられます。すき間が玉の数よりも1つ少ないことに注意しましょう。
((図))
要するに4つのすき間から2個を選ぶ場合の数になるので、
4C2=10通り になります。
ここが空きOKと空きNGでやり方が一番変わるところですね。
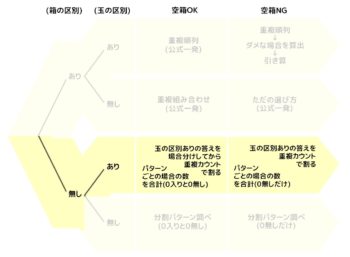
C:玉だけ区別あり
三番目が一番厄介なパターン「玉だけ区別あり」です。「生徒を区別の無い三つの部屋に組分けする」などもこのパターンです
このパターンは解法が二つあり、どちらも他のパターンの計算をして利用しないといけないので面倒です。
まず解法1で空きOKと空きNGを説明し、解法2は記事の最後に別解としてのせています。。
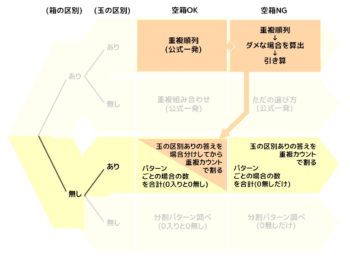
C-1:空きOKの場合
→パターンA(玉区別あり)の答えの場合分けしてから重複カウントで割る:難易度★★★
色が違う5個の玉を3つの箱に分けます。全部で何通りありますか?
使用するのはパターンA:「空き箱NGで色の違う5個の玉をABC3つの箱に分ける」問題の途中過程で出した数値です。
パターンA-1(空きOK)の場合が全部で$3^5$=243通りで、そこから空き箱が1個の場合(90通り)と2個の場合(3通り)を引いてA-2(空きNG)の答え(150通り)を出しました。
その内訳をもう一度整理するとこうなります。
1つの箱に5個入っている:3通り
2つの箱に 〃 :90通り
3つの箱に分かれている:150通り
合計すると$3^5$=243通り
玉だけ区別あり、つまり箱に区別が無くなると、この3つの数(3,90,150)をそれぞれの重複カウント数で割ることになります。
X:1つの箱に5個入っている場合は、重複カウントは3通り(Aに全部、Bに全部、Cに全部)なので箱の区別を無くすと3÷3=1通りになります。
Y:2つの箱に5個入っている場合は、重複カウントは6通り(3箱なので3!)なので箱の区別を無くすと90÷6=15通りになります。
Z:3つの箱に分かれている場合も、重複カウントは6通り(3箱なので3!)なので箱の区別を無くすと150÷6=25通りになります。
X:1箱に5個:3通り→(÷3)→1
Y:2箱に :90通り→(÷6)→15
Z:3箱に :150通り→(÷6)→25
X:Y:Z:の合計:243通り→41通り
これを合計して、1+15+25=41通りになります。
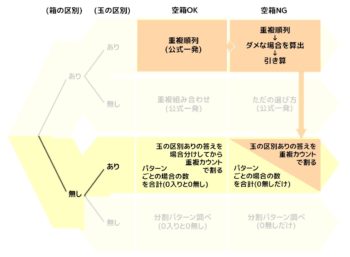
C-2:空きNG
→パターンA-2(玉区別あり空きNG)の答えを重複カウントで割る:難易度★★★
色が違う5個の玉を3つの箱に分けます。全部で何通りありますか?但し空き箱が無いようにします。
今度も箱の区別がなくなりますが空き箱がNGなので、先程のX:Y:Z:のうち、Z:(3箱に5個が分かれている)だけが答えです。
X:1箱に5個:3通り
Y:2箱に :90通り
Z:3箱に分かれている:150通り→(÷6)→25
色の違う5玉がABC3つの箱に分かれている場合が150通りで、重複カウントは6通り(3箱なので3!)なので箱の区別を無くすと150÷6=25通り
D:箱も玉も区別なし
最後は箱も玉も区別がないパターンです。
これは数字の分割方法を調べるだけです。
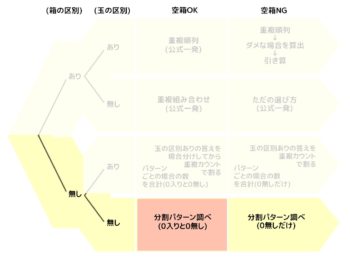
D-1:空きOK
→分割のパターン調べ:難易度★☆☆
5個の玉を3つの箱に分けます。全部で何通りあるか?空き箱があっても構わない
これは「5」という数字を3つに分割するやり方が何通りあるかを数えるのと同じです。3つの中に0が入っていても構いません。こうなります。
(0,0,5)(0,1,4)(0,2,3)(1,1,3)(1,2,2)
この5通りが答えになります。
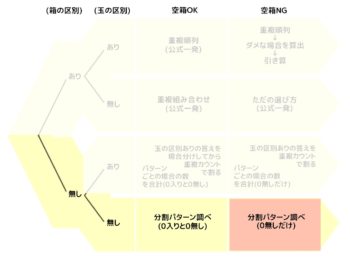
D-2:空きNG
→分割パターン調べ:難易度★☆☆
5個の玉を3つの箱に分けます。全部で何通りありますか?但し空き箱が無いようにします。
これも分け方のパターンで、今度は0が入ってはいけないので…
(0,0,5)(0,1,4)(0,2,3)(1,1,3)(1,2,2) こうなります。
この2通りが答えになります。
以上で8パターンの解法を一通り説明しましたが、パターンC:には別解があって、こちらもマスターしたほうが良いと思われるので紹介します。
C:玉だけ区別ある場合の別解
パターンCの別解は「D:部屋も玉も区別がない」の数値を再利します
C-1′:空きOK(別解)
→分割パターン調べ+分配計算:難易度★★★
色が違う5個の玉を3つの箱に分けます。全部で何通りありますか?
❶まず分け方がいくつあるか調べます。
これはパターンD:で数えて5通りでした。
(0,0,5)(0,1,4)(0,2,3)(1,1,3)(1,2,2)
❷この5通りそれぞれについて、分配方法が何通りあるか調べます。それぞれが独立した問題の感覚で解いていきます。他の基本問題にも利用できるます。
➀(0,0,5)の場合
色が違う5個の玉を3つの箱に0個、0個、5個に分けます。全部で何通りありますか?
→箱に区別がないので1通り
➁(0,1,4)の場合
色が違う5個の玉を3つの箱に0個、1個、5個に分けます。全部で何通りありますか?
→1個の箱に入れる玉を選べばよいので5C1=5通り
③(0,2,3)の場合
色が違う5個の玉を3つの箱に0個、2個、3個に分けます。全部で何通りありますか?
→2個の箱に入れる玉を選べば良いので5C2=10通り
④(1,1,3)の場合
色が違う5個の玉を3つの箱に1個、1個、3個に分けます。全部で何通りありますか?
これは独立した問題として出題もされますね。
→5個から1個選ぶのが5C1、残りの4個から1個選ぶのが4C1,最後が3C3で、同じ数の部屋2つを重複して数えているので2!で割る、でした。
5C1×4C1×3C3÷2!=5×4×1×12=10通り
(簡単に考えると3個選べば残りは決まるので5C3=5C2=10)
⑤(1,2,2)の場合
色が違う5個の玉を3つの箱に1個、2個、2個に分けます。全部で何通りありますか?
これも独立した問題として出題されますね
→1個の箱に入れるのを選ぶのが5C1,2個の箱に入れる玉を選ぶのが4C2,残りは2C2,同じ数の箱の重複カウントが2!あるので
5C1×4C2×2C2÷2!=5×4×32×1×1×12=15通り
❸今の5つの場合を合計すると答えです。
1+5+10+10+15=41通り
C-2′:空きNG(別解)
→分割パターン調べ+分配計算:難易度★★★
色が違う5個の玉を3つの箱に分けます。全部で何通りありますか?但し空き箱が無いようにします。
❶まず分け方がいくつあるか調べます。これもパターンD:の空きNGで調べました。
(0,0,5)(0,1,4)(0,2,3)(1,1,3)(1,2,2)
0があってはいけないので、2通りしかありません。
❷この2通りについて、分け方が何通りあるか調べます。
➀(1,1,3)の場合
色が違う5個の玉を3つの箱に1個、1個、3個に分けます。全部で何通りありますか?
→5個から1個選ぶのが5C1、残りの4個から1個選ぶのが4C1,最後が3C3で、同じ数の部屋2つを重複して数えているので2!で割る
5C1×4C1×3C3÷2!=5×4×1×12=10通り
➁(1,2,2)の場合
色が違う5個の玉を3つの箱に1個、2個、2個に分けます。全部で何通りありますか?
→1個の箱に入れるのを選ぶのが5C1,残りの4個から2個選ぶのが4C2,残りは2C2,同じ数の箱の重複カウントが2!あるので、
5C1×4C2×2C2÷2!=5×4×32×1×1×12=15通り
❸2つの場合を合計すると答えです。
10+15=25通り
以上で全ての説明が終了です。お疲れ様でした!
次のステップへ
組分け問題が整理できましたか?場合の数の学習は一通りです。確率に進んで下さい。
最後まで読んでいただきありがとうございました。この記事があなたの役に立てたなら嬉しいです♪