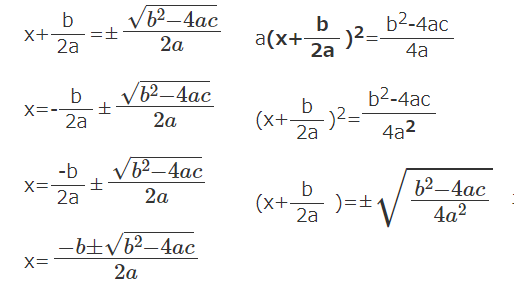2次方程式】解の公式の証明【中3・数Ⅰ

 

中3・高1で「解の公式の証明が分からない…」という方へ

確かに面倒くさいのですが、考え方は「2次方程式の平方完成」そのものなので、「平方完成」が分かれば理解の準備はできています。

この記事では東大卒講師歴20年超の図解講師「そうちゃ」が「平方完成」「解の公式の証明」を分かりやすく解説します。

記事を読んで真似すれば「解の公式の証明」はもう大丈夫でしょう♪

解の公式

2次方程式ax²+bx+c=0の解xは x=$\frac{-b±\sqrt{b^2-4ac}}{2a}$ で導かれる。

これが解の公式(quadratic-formula)です。

練習
2x²+3x+1=0の解を求める

x=$\frac{-b±\sqrt{b^2-4ac}}{2a}$ にa=2,b=3,c=1を代入して

x=$\frac{-3±\sqrt{3^2-4×2×1}}{2×2}$=$\frac{-3±\sqrt{9-8}}{4}$=$\frac{-3±1}{4}$=-3+14,-3-14=-24,-44=-1,-12

解の公式を確認したところで、証明に行きたいのですが、その前に…

証明の前提～平方完成

解の公式を導くには「平方完成」を用いるので、平方完成が完璧に分かるようにしておく必要があるので確認です

「完璧に分かるよ！」という人はジャンプして下さい

二次係数が1の場合

基本作業の確認です

(例題1)
2次方程式 x²+6x+5=0 を平方完成して解きなさい

(解説)
x²+6x+5=0
(x²+6x)+5=0　まず定数項以外をカッコでまとめる

ここで、(x²+6x+□)=(x+◇)² にできるような□を考えると、(x²+6x+9)=(x+3)²  と思いつくでしょう。
(理屈で考えると  ◇=6÷2=3 で □=◇²=9 です)

(x²+6x)+5=0　(x²+6x+9)と比べると9が足りないので…
(x²+6x+9)+5=9　9を両辺に加える
(x²+6x+9)=9-5　左辺の5を右辺に移項
(x+3)²=4　(x²+6x+9)を(x+3)²に変形

「x²+6x+5=0」が「(x+3)²=4」になりました。
これが「平方完成」でした。ここからxを求めます

(x+3)²=4
x+3=±$\sqrt{4}$　平方根にする
x+3=±2
x=-3±2　左辺の3を移項
x=-1,-5　答えが出ました。

分かりましたね？

二次係数が1以外の場合

ちょっと手間が増えますが、これが出来れば解の公式の証明まであと一歩です

(例題2)
2次方程式 2x²+12x+4=0 を平方完成して解きなさい

2x²+12x+4=0　x²に係数2がついている
2(x²+6x)+4=0　まず定数項「5」以外を2でくくる

ここで、(x²+6x+□)=(x+◇)² にできるような□を考えると、例1と同じく(x²+6x+9)=(x+3)²  で、左辺のカッコは(x²+6x+9)と比べると9が足りない

2(x²+6x)+4=0
2(x²+6x+9)+4=18　左辺のカッコの中に9を加えるので、右辺には9x2=18を加えることに注意

2(x²+6x+9)=18-4　左辺の4を右辺に移項
2(x+3)²=14　(x²+6x+9)を(x+3)²に変形

「2x²+12x+5=0」が「2(x+3)²=14」になりました。「平方完成」終了♪

2(x+3)²=14
(x+3)²=7　両辺を2で割る
x+3=±$\sqrt{7}$　平方根にする
x=-3±$\sqrt{7}$　左辺の3を移項して答えです

これでもう解の公式の証明ができます。

解の公式の証明

二次方程式の一般形「ax²+bx+c=0」を上の平方完成例2(二次の係数が1でない場合)と同じように変形していきます。

ax²+bx+c=0　x²に係数aがついている
a(x²+bax)+c=0　定数項以外をaでくくる

ここで、(x²+bax+□)=(x+◇)² にできるような□を考えると、  ◇=ba÷2=b2a で □=◇²=b²4a² です

a(x²+bax)+c=0
a(x²+bax+b²4a²)+c=b²4a　左辺のカッコ内にb²4a²を加えます。右辺に加えるのはaをかけたb²4aになることに注意

a(x²+bax+b²4a²)+c=b²4a

a(x²+bax+b²4a²)=b²4a-c　cを右辺へ

a(x²+bax+b²4a²)=b²-4ac4a–4ac4a　-cを4aで通分

a(x²+bax+b²4a²)=b²-4ac4a　右辺を仮分数にまとめる

a(x+b2a)²=b²-4ac4a　左辺のカッコを( )²の形に

(x+b2a)²=b²-4ac4a²　両辺をaで割る

(x+b2a )=±$\sqrt{\frac{b^2-4ac}{4a^2}}$　平方根にする

x+b2a=±${\frac{\sqrt{b^2-4ac}}{2a}}$

x=-b2a±${\frac{\sqrt{b^2-4ac}}{2a}}$　b2aを移項

x=-b2a±${\frac{\sqrt{b^2-4ac}}{2a}}$

x=${\frac{-b±\sqrt{b^2-4ac}}{2a}}$　解の公式ができました！

証明は以上です！