「三角比、わけ分かんない」という高校生の皆さんへ。東大卒講師歴20年の管理人が分かりやすくまとめます。確認テストで定着を図れるので、三角比が得意になりますよ!
目次(クリックでジャンプ)
三角比の意味
「三角比」分けわからない言葉ですが、難しい意味ではありませんよ。「直角三角形の三辺の比」という意味です♪
三角比の定義
三角比の例
辺a=4,b=3,c=5の直角三角形ABCがあるとき、底角のうち直角でない方∠ABCをθとします。
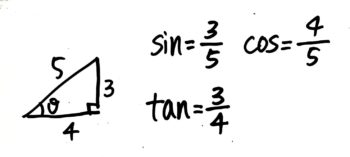
この時、三辺の比を分数の形にして、35を「sinθ」、45を「cosθ」、34を「tanθ」と決めます(昔の人がそう決めました。)
三辺がx,y,rである直角三角形の
底角の直角でない方の角度をθとする時
➀sinθ=yr ➁cosθ=xr ➂tanθ=yx
((図))
おぼえ方
決めたと言われても、覚えにくいですね。そこで有名な覚え方があります。
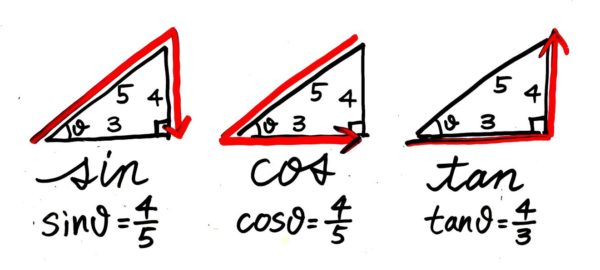
サイン、コサイン、タンジェントの頭文字を筆記体で書くときの手の動きで、分母→分子の順に数字を拾っていきます。
まず、三辺が分かっている直角三角形を見て、sin,cos,tanが言えるようにしましょう!
作成中
三角比の目的
ちなみに、なんでこんなことするの?かというと、いろいろな直角三角形の比(つまり形)をデータとして保管して利用するためです。例えば「cosθが45の三角形」といえば図のような「3:4:5」の三角形と分かりますね。
ただ、実際に土木・建築などで三角形を使う場合は、地面から建造物を見上げた角度(さきほどのθ)を測定するので、直角三角形の形をθで分類するのが都合が良いです。つまり「θが30°の三角形の形のデータを知りたい」と思うのです。
そこで、三角比はθの角度で記録・整理してあります。教科書や問題集の巻末を見ると三角比が表の形でのっています。例えば「見上げた角度が20°になるような三角形の形を知りたい」場合は、表の20°を見ると、分かります。
三角比の利用
三角比の「逆」
実際にさっき作った三角比を変形して、各辺をsin,cos,tanを用いて表してみます。
➀sinθ=yr の両辺に r をかけて y=rsinθ
➁cosθ=xr の両辺に r をかけて x=rcosθ
➂tanθ=yx の両辺にxをかけると y=tanθ
➀x=rcosθ ➁y=rsinθ ➂r=xtanθ
問題
例題1(➀➁)
例題2(➂)
作成中(坂の問題)
三角比の相互関係
ここから、さっきよりも抽象的・数学的な世界に入ります。
相互関係を導く
またまた3:4:5の直角三角形を思い出します。
(図)
sinとcosを使う頻度が高いので、tanもsinとcosで表したい。
sinθ=35 ,cosθ=45 ,tanθ=34 =35÷45 なので、
tanθ=sinθcosθ…➀ と表せます
また、ピタゴラスの定理より、
sinθ2+cosθ2=1…➁ です
➁で半分以上の問題が解けますが、例えばtanしか分からないときのためにtanの入った式も欲しいですね。そこで➁を変形します。
➁全体をcosθ2で割ります。
sin2θcos2θ+cos2θcos2θ=1cos2θ
➀を2乗した式:tan2θ=sin2θcos2θ を代入して
1+tan2θ=1cos2θ
tanしか分からない時も、この式を使えばcosが分かるので、tan→cos→sin と出すことができますね。
➀tan=sinθcosθ (t=sc)
➁sin2θ+cos2θ=1 (s2+c2=1)
➂1+tan2θ=1cos2θ (1+t2=1c2)
問題
例題
作成中
余角(90-θ)の定理
正直言うと、これは後で「三角比と座標(単位円)」と一緒に学んだ方が分かりやすいです。ココにも同じ内容を書いてありますので、飛ばしてよんでも平気です。
例30°の直角三角形と60°の直角三角形
sin(90-θ)=cosθ
cos(90-θ)=sinθ
tan(90-θ)=1tanθ
「sinとcosが入れ替わる」イメージです。
sin(90-θ)=cosθ cos(90-θ)=sinθ
tan(90-θ)=1tanθ
作成中
三角比の拡張
ここからは関数で使っている座標上で三角比を扱います。個人的には、このイメージを持てれば三角比はラクチンだとと思います。
単位円~座標に三角比を導入
座標平面上で原点を中心に半径1の円(単位円)を書きます。
((図))
そして、中心から円周に「腕」を伸ばして、x軸(の正方向)と作る角度をθとします。
((図))
この時の腕の先端の座標(x,y)を考えます。腕の先端から垂線をおろすと、x軸と合わせて直角三角形ができます。この直角三角形の三辺は「1」「x」「y」です。
((図))
ここで、上でやった「三角比の逆」を思い出しましょう。
➀x=rcosθ ➁y=rsinθ ➂r=xtanθ
r=1なので、➀よりx=rcosθ=cosθ ➁よりrsinθ=sinθ
です。つまり「腕」の先端の座標は(cosθ,sinθ)になります。
単位円→原点を中心に半径1の円
角度θの「腕」の先端の座標(cosθ,sinθ)
理屈がよくわからなくても(分かって欲しいですが…)、この定理は絶対暗記して下さい。これを暗記すれば三角比は半分終了です♪(使って問題を解いているうちに分かってきますからね!)
補角(180-θ)の定理
θの「腕」と180-θの「腕」
例30°の腕と150°の腕
y軸対称になっているので、x座標(cos)は正負反転、y(sin)はそのまま
sin(180-θ)=sinθ
cos(180-θ)=-cosθ
腕の傾き(tan)も正負反転する
tan(180-θ)=-tanθ
sin(180-θ)=sinθ
cos(180-θ)=-cosθ
tan(180-θ)=-tanθ
問題で練習
余角(90-θ)の定理
上の方にもありましたが、補角の定理と学んだ方が分かりやすいので、再度紹介します。
例30°の直角三角形と60°の直角三角形
sin(90-θ)=cosθ
cos(90-θ)=sinθ
tan(90-θ)=1tanθ
「sinとcosが入れ替わる」イメージです。
sin(90-θ)=cosθ
cos(90-θ)=sinθ
tan(90-θ)=1tanθ
等式を満たすθ(三角比の方程式)
座標上での三角比の相互関係
上でやったのとほとんど変わりません
三角形と正弦定理・余弦定理
三角形ABCの辺と角の名称
例30°の直角三角形
正弦定理
定理を導く
例30°の直角三角形
asinA=bsinB=csinθ=2R
三角形ABCの外接円の半径をRとする時
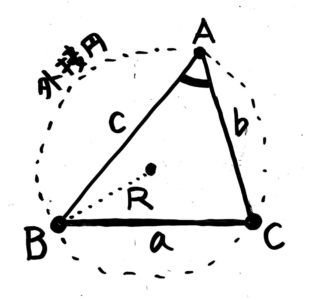
asinA=bsinB=csinθ=2R
定理を実戦的に拡張
「生の」正弦定理そのままでは用途が限られるので、問題を解く際に直接使えるような形に変形(拡張)しておきましょう
正弦定理の基本の形
三角形ABCの外接円の半径をRとする時、
asinA=bsinB=csinC=2R
これの一つを取り出して…
asinA=2R
左辺の分母と右辺をクルッと入れ替える。
a2R=sinA
更に左辺と右辺を入れ替えると…
sinA=a2R
対辺の長さと外接円の半径からから角のsinを出す式になりました(角度そのものではなく正弦が分かることに注意
)。
三角形ABCの外接円の半径をRとする時、
sinA=a2R
sinB=b2R
sinC=c2R
さらに比の形にします
sinA:sinB:sinC=a2R:b2R:c2R
右辺は比なので、全部に2Rをかけて分母を払っても成り立ちます。
sinA:sinB:sinC=a:b:c
便利な式ができました。角度の比ではなくsinの比であることに注意して下さい。
三角形ABCにおいて
sinA:sinB:sinC = a:b:c
(角度のsinの比は三辺の比と等しい)
この3つを正弦定理の拡張としてセットで覚えましょう。
三角形ABCの外接円の半径をRとする時、
asinA=bsinB=csinC=2R
三角形ABCの外接円の半径をRとする時、
sinA=a2R
sinB=b2R
sinC=c2R
三角形ABCにおいて
sinA:sinB:sinC = a:b:c
(角度のsinの比は三辺の比と等しい)
練習問題
(作成中)
余弦定理
定理を導く
例 : : の三角形(底辺 )
a2=b2+c2-2bc cosθ
b2=a2+c2-2ac cosθ
c2=a2+b2-2ab cosθ
このような定理を覚える際は、成り立ち・証明を覚えるよりも、まず「どういう法則か」つまり「何から何を導けるのか」「何が分かると何が分かるのか」を日本語で覚えると、実践的に定着しやすい
余弦定理の場合は「2つの辺の長さと挟む角(の余弦)が分かれば対辺の長さが分かる」定理です。図にするとこうなります。
二辺と挟む角から対辺の長さを求める
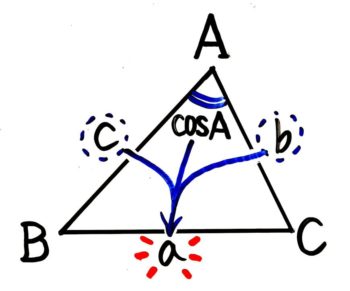 a2=b2+c2-2bc cosA
a2=b2+c2-2bc cosA
b2=a2+c2-2ac cosB
c2=a2+b2-2ab cosC
余弦定理の拡張
正弦定理を拡張して覚えたように、余弦定理も実践的な形に拡張して覚えておきましょう。
まず先程の余弦定理本体。これは辺を求めるのに使います。
a2=b2+c2-2bc cosθ
b2=a2+c2-2ac cosθ
c2=a2+b2-2ab cosθ
これを「cos=」の形に変形すると、こうなります。これは角度(cos)を求めるときに使えますね。
三辺から好きな角度のcosを求める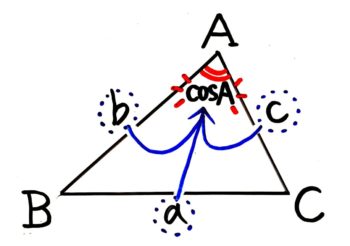 cosA=b2+c2-a22bc
cosA=b2+c2-a22bc
cosB=a2+c2-b22ac
cosC=a2+b2-c22ab
余弦定理はこの2つをセットで覚えておきましょう
練習問題
(作成中)
二つの定理を併用する
一つの問題で正弦定理と余弦定理の両方を使うことがよくあります。はじめは「どちらを使ったらいいのかよく分からない!」でしょうから、使い分けの基準も知っておきましょう。
二つの定理の使い分けの基準
簡単に言うと、三角形の形を定める条件(中学のときの合同条件を思い出す)がそろっていれば余弦定理が使えます。
だめな場合は正弦定理を使いますが、三角形の形は決まりません(「形が決まらない」の意味はこの後分かります)。
まとめるとこうなります。
●(三角形を決める条件が揃っている)
○三辺が分かっている→余弦定理
○二辺と挟角が分かっている→余弦定理
○一辺と両端の角が分かっている→正弦定理
●(条件がそろっていない)
○二辺と非挟角が分かっている→正弦定理(答えが二通りでる)
○三つの角だけが分かっている→正弦定理(辺の比だけが分かる)
つまり、条件がそろっていれば余弦定理(+正弦定理)か正弦定理を使い、そろっていなければ正弦定理を使って答えが複数通り出ます。
では実際に問題をといてみましょう
正弦定理・余弦定理の利用
角度を求める問題
(1)三辺から三つの角度を求める
一つの角度を余弦定理で出す→残りのうち一つを正弦定理で出す→残りは180から引き算
(2)二辺挟角から残りの辺と角度を求める
残りの辺を余弦定理で出す→残りの角度のうち一つを正弦→残りは180引き算
長さを求める
(1)三辺が分かっている三角形ABCにおいて、頂点Aから対辺の中点Dへの線ADの長さを求める
→三角形ABCと三角形ABDでBについて余弦定理の式を作り、=で結んで方程式を作る。
(1)三辺が分かっている三角形ABCにおいて、頂点Aから対辺を内分する点Dへの線ADの長さを求める
→三角形ABCと三角形ABDでBについて余弦定理の式を作り、=で結んで方程式を作る。
(2)三辺が分かっている三角形において、頂角の二等分線ADの長さを求める
→中線定理でBDとDCを求める。あとは(1)と同じ
(3)二辺挟角が分かっている三角形において、頂角の二等分線の長さを求める
→
三角形の形状を判別する
三角形の形と条件式
この問題を解く時は、前もって結論を頭に入れておいて、このどれかに変形するんだな、と思いながら考えます。
「a=b」→二等辺
「a=b または a=c」→二通りの二等辺三角形
「a=b かつ a=c」→正三角形
「a=b=c」→正三角形
「a2+b2=c2 」→cを斜辺とする直角三角形
「a2+b2=c2 かつ a=b」→a=bの直角二等辺三角形
cが一番長い辺の時
「a2+b2<c2」→鈍角三角形
「a2+b2>c2」→鋭角三角形
条件式を導く等式の形
(1)移項して完成
a-b=0
a=b →二等辺三角形
a2-c2=b2
a2+b2=c2 →cを斜辺とする直角三角形
(2)因数分解で2つの条件
a2-ab-ac-bc=0
(a-b)(a-c)=0
a-b=0 かつ a-c=0
a=b かつ a=c →正三角形
実際の問題を解く
平面空間への応用
三角形の面積
面積その1(二辺挟角から)
例
S=12bcsinA
S=12bcsinA=12acsinB=12absinC
これは「二角挟辺パターン」なので、余弦定理でcosAを出してs2+c2=1でsinを出してから使います。その流れ自体を拡張した公式として覚えておくと良いでしょう。
cosA=b2+c2-a22bc
sinA=$sqrt{1-cosA^2}$
S=12bcsinA
sinA=$sqrt{1-cos^2}$
その2(内接円から)
これは高校入試で勉強した人も多いでしょう。
内接円の半径をrとした時
S=12r(a+b+c)
三角形ABCの内接円の半径をrとした時
S=12r(a+b+c)
その3(三辺から):ヘロンの公式
三角形ABCで、s=a+b+c2とおくとき(小文字のsです)
S=$sqrt{s(s-a)(s-b)(s-c)}$ になります。
三角形ABCで、s=a+b+c2とすると
S=$sqrt{s(s-a)(s-b)(s-c)}$
空間図形
次のステップへ
三角比は分かりましたね?高校2年生の方は「三角関数」へ進みましょう!
最後まで読んでいただきありがとうございました。
この記事があなたの役に立てたなら嬉しいです♪
